本文中我越过基本概念,直接说理解。
傅里叶变换通常关注的是不随时间衰减的信号,或者系统在特定频率下的响应。而拉普拉斯信号更多关注实际有阻尼的系统中,系统响应的长期变化。两者有紧密的联系。
时域,频域(傅里叶形式)与复频域(拉普拉斯形式)表达式是对同一组信号的不同表述。再往大说一点,傅里叶变换,拉普拉斯变换,甚至包括不知道有没有机会讲的小波变换,都在做一件事,将信号在已知的基空间做投影,唯一的区别是基的选取不同。
傅里叶变换的基为三角函数,为什么要选三角函数作为傅里叶变换的基,因为三角函数的一大特点是,经过线性时不变系统的操作(加减,倍乘,倍除,积分,求导)后,不改变波形,仅改变相角和幅值。这就给我们提供了一个巨大的好处,那就是在分析线性时不变系统时,仅通过信号的相角和幅值指标就能还原信号,可以忽略基函数波形本身。
傅里叶反变换
傅里叶反变换过程是通过一系列三角函数叠加生成时域上的任意周期函数。
假设原函数 是一系列余弦函数的叠加:
(1)
将上述定义推广至连续的情况:
(2)
是角频率的实函数,也就是频谱。对傅里叶变换的初级理解可以止步与此。
但是上式中完全没有体现相角的变量,也就是说,目前我们没有办法调整每个频率下的余弦函数的超前或滞后角度。
为了同时控制每个角频率下幅值与相角的变化,即
将(2)中只能表示长度的实函数 换成能同时表示长度与方向的虚函数 。
即表示 角频率下的余弦函数基不但幅值变化为 倍,相角也要移动 度,幅值增益 和相角 都是角频率 的函数。
由于 的系数已经从实数 变成了复数 ,为了使余弦函数与复数的乘积有意义,我们必须将余弦函数 替换成对应的极坐标形式 。(2)变为:
(3)
接下来证明(3)的正确性。
根据欧拉公式:
(3)化为:
这里先不加证明的给出一个结论, 是频域上的偶函数, 是频域上的奇函数。注意函数相乘的奇偶性规律:
奇偶为奇,奇奇为偶,偶偶为偶。
因此上式中的虚数部分都是奇函数,在全频域的积分为零。
根据三角函数公式:
可见,我们实现了可以单独控制每个角频率下余弦函数的幅值与相角的功能。
傅里叶变换
理解了上面的傅里叶反变换过程,再倒推傅里叶正变换就变得非常简单了。
(4)所代表的傅里叶反变换的过程可以这样理解,我们想知道 ,对于每个角频率 ,时域函数 中包含了“几个”傅里叶变换的基函数 ,这里的“几个”不光是有数值的含义( 的幅值),也有相角的含义( 的角度)。因此,“几个”在这里是个复数,即 。
这个“几个”不是瞬时值,而是在全时域内的稳定结果。当原函数 与傅里叶基函数 的频率 不重合时, 在 的值为零,举例如下:
当原函数(绿色)为 ,而傅里叶基函数(红色)为 时,两者的乘积在全时域的累积是0。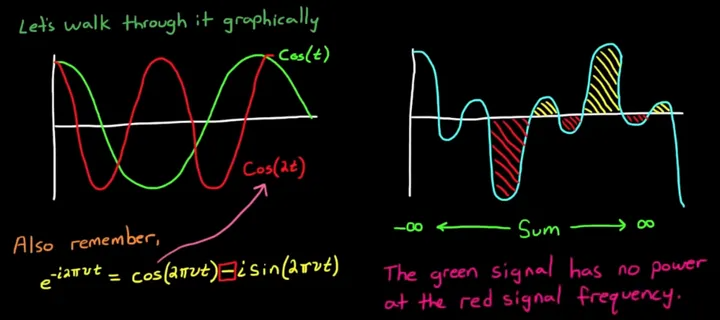
当原函数(绿色)为 ,而傅里叶基函数为 时。当且仅当 时,存在不为零的 。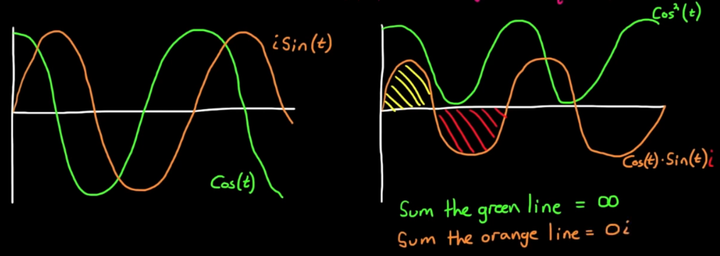
当 时,
同理,当 时, 。
注意冲击函数 的如下性质:
因此, 。
验证上述傅里叶变换结果:
注意冲击函数的面积为1:
因此,
拉普拉斯变换
理解了傅里叶变换,拉普拉斯变换的意义就变得容易理解了。
傅里叶变换中的基函数是 ,能用它拟合的函数具有共同特征,那就是,各个频率下的三角函数分量不随时间衰减。这个假设具有明显的局限性,要么是理想没有阻尼的系统,要么是研究有阻尼的系统对特定频率的瞬时响应(bode图)。
因此,我们需要对傅里叶变换的基函数进行拓展:
称为拉普帕斯算子。
这样,我们就有了幅值(能量的开方)可以随时间按照指数规律变化的基函数, 的正负决定基函数究竟是不断增大还是逐渐收敛。因此,拉普拉斯变换的定义域( )是一个二维平面,叫做s域(s plane),每个自变量 包括实轴 和虚轴 两个维度。可见,傅里叶变换是拉普拉斯变换在 这条线上的“切片”。
拉普拉斯变换后的结果和傅里叶变化一样,是一个复函数,唯一不同的是,傅里叶变化结果的复函数的模值是时不变的,而拉普拉斯变化结果的复函数的模值是对应傅里叶变化的复函数的模值乘以 即随时间变换。


评论 (0)